Distance calculation
 With the growing distribution of GPS devices and tools such as Google Earth or GeoPosition it is easy to determine the geographical coordinates of interesting points on the earth's surface. This article shows how to determine the exact linear distance between two points using their coordinates.
With the growing distribution of GPS devices and tools such as Google Earth or GeoPosition it is easy to determine the geographical coordinates of interesting points on the earth's surface. This article shows how to determine the exact linear distance between two points using their coordinates.
Geographic coordinates
The Earth's surface resembles the surface of a sphere. Each point on the earth's surface can thus be uniquely described by two coordinates: latitude and longitude.
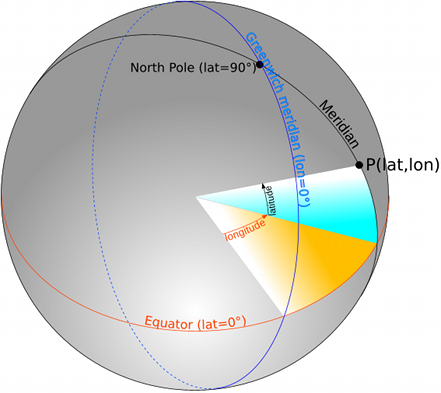
The latitude (abbreviated: lat) describes the angle that spans itself between the center of the earth, the searched point P and the equator (blue area in Fig. 1). Points on the equator have always a latitude of 0, while the north pole has a latitude of 90 degrees and the south pole -90 degrees. The curve that passes through points of equal latitude, is called circle of latitude or parallel.
The longitude (abbreviated: lon) is the angle between the center of the earth, the searched point P and the prime meridian (yellow area in Fig. 1). A meridian passes through the North Pole, South Pole and all points of equal longitude. The meridian that runs through the old Greenwich Observatory was arbitrarily assigned a value of 0, making it the prime meridian or Greenwich meridian. Points east of Greenwich have a longitude between 0 and 180 degrees and points west of it from 0 to -180 degrees. The meridians -180 and 180 degrees are identical and represent virtually the extension of the prime meridian.
Examples of geographic coordinates
| Place | Latitude | Longitude in degrees |
|---|---|---|
| Rüsselsheim Station | 49.9917 | 8.41321 |
| Rüsselsheim Opel bridge | 50.0049 | 8.42182 |
| Berlin Brandenburg Gate | 52.5164 | 13.3777 |
| Lisbon Tagus bridge | 38.692668 | -9.177944 |
Simple distance calculation
First, the distance between Rüsselsheim station and Opel bridge is to be determined. The simplest approach is to take a map of Rüsselsheim with marked lines of latitude and langitude (Fig. 2).
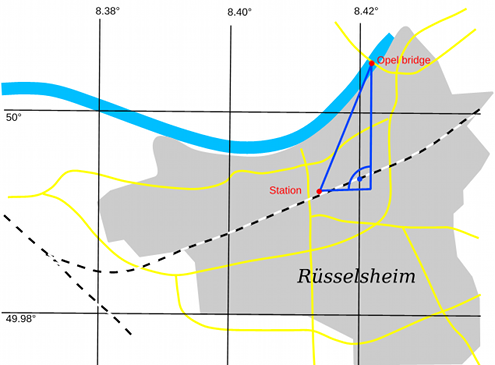
As you can see, the meridians and parallels are straight lines which are parallel and perpendicular respectively to each other. We can therefore view the Earth's surface as a plane and use for this relatively small area the Pythagorean Theorem for distance calculation:
distance = sqrt(dx * dx + dy * dy)
with distance: Distance in kilometer (km)
dx = 71.5 * (lon1 - lon2)
dy = 111.3 * (lat1 - lat2)
lat1, lat2, lon1, lon2: Latitude, Longitude in degrees
When specifying the length and width in degrees, there is the distance in kilometers. The constant 111.3 is the distance between two circles of latitude in km and 71.5 is the average distance between two meridians in our latitudes.
Improved method
While the distance between two circles of latitude is always constant 111.3 km, the distance between two meridians varies depending on the latitude: At the equator, it is also 111.3 km, but at the poles, however 0. More precisely, their distance is calculated by the formula
111.3 * cos(lat)
This can be incorporated into the calculation formula. The value of lat is chosen from the average of lat1 and lat2.
In the calculation using a computer it is important to remember that although most programming languages provide the cosine function, it is usually expecting the angle in radians - not in degrees! The conversion from degrees to radians is done according to the relation:
1° = π/180 rad ≈ 0.01745
The full, improved formula for the distance calculation is then:
distance = sqrt(dx * dx + dy * dy) with distance: Distance in km dx = 111.3 * cos(lat) * (lon1 - lon2) lat = (lat1 + lat2) / 2 * 0.01745 dy = 111.3 * (lat1 - lat2) lat1, lat2, lon1, lon2: Latitude, Longitude in degrees
Exact distance calculation for the surface of a sphere
Unfortunately, these simple methods fail at greater distances. The reason for this is obvious if you, for example, look at a map of Europe (Fig. 3):
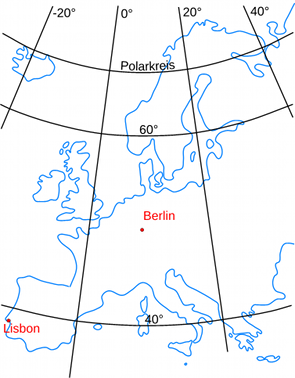
The parallels and meridians do no longer form a rectangular grid here. This is due to the spherical shape of the earth. But it is impossible to unroll a spherical surface into a plane without distortions. While one can ignore the distortion on small areas such as a street map, a map of Europe can no longer produced in this way.
You have to use here methods of spherical trigonometry and take into account the definition of latitude and longitude from above.
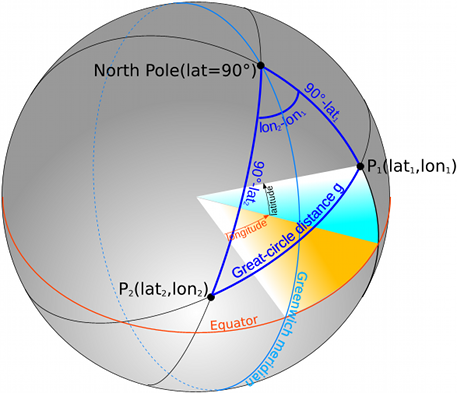
Fig. 4 shows again the earth as sphere, but now with two marked points P1 and P2, whose distance is to be determined. This (shortest) distance is also called great circle distance. The points P1 and P2 form a spherical triangle together with the North Pole. From this two sides and the angle are known: The length of the side is equal to the distance of the point from the North Pole, so 90 degrees minus its latitude. The included angle is calculated from the difference of the lengths of the two geographical points.
Thus, it is now possible to determine the length of the third side, which is this great circle arc. The formula uses the cosine rule:
cos(g) = cos(90° - lat1) * cos(90° - lat2) + sin(90° - lat1) * sin(90° - lat2) * cos(lon2 - lon1) with g: Great circle distance lat1, lat2, lon1, lon2: Latitude, Longitude
Since cos(90° - a) = sin(a) and sin(90° - a) = cos(a) applies, the formula simplifies to:
cos(g) = sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1)
To get the distance in kilometers, one must still form the arc cosine and multiply the result by the radius of the earth:
dist = 6378.388 * acos(sin(lat1) * sin(lat2) + cos(lat1) * cos(lat2) * cos(lon2 - lon1)) with dist: distance in km
The formula applies to the indication of the angle in radians, which is the standard for most programming languages. If we compute with a pocket calculator, which is set to degrees, then we have to use the value 6378.388 * π / 180 = 111.324 instead of 6378.388.
Calculation with the Haversine formula
The calculation formula based on the spherical triangle is mathematically correct, but leads to erroneous results at very small distances of less than one meter. The reason for this is that computers usually do not calculate with arbitrary precision. For example when using the C++ data type double, the precision is limited to 15 significant digits. At very small distances, this means that the result is always zero due to rounding errors.
The Haversine formula leads to better results here. It also calculates the mathematically correct distance on the sphere's surface, but it is numerically better-conditioned for small distances:
dLat = lat2-lat1 dLon = lon2-lon1; a = pow(sin(dLat/2.0), 2) + pow(sin(dLon/2.0), 2) * cos(lat1) * cos(lat2) dist = 6378.388 * 2.0 * atan2(sqrt(a), sqrt(1.0-a)) with dist: distance in km
Evaluation of methods
Which of the above methods should now come to application, depends on several factors:
- Distance of the points
- Required accuracy
- Cost of calculation (i.e., consumption of time, CPU cycles, ...)
On fast PCs the point of cost differences is now much less relevant. But if you have to type in the formulas on the pocket calculator, the time plays a major role.
To compare the accuracy of the formulas, they are now used to calculate the distance between the Rüsselsheim station and the Opel Bridge and, on the other hand, between Berlin and Lisbon. In addition, the distance between adjacent points with a distance of 1 meter and 1 centimeter is calculated.
| Distance | Simply | Improved | Cosine rule | Haversine |
|---|---|---|---|---|
| Rüsselsheim Station - Rüsselsheim Opel bridge | 1.593 km | 1.593 km | 1.593 km | 1.593 km |
| Berlin Brandenburg Gate - Lisbon Tagus bridge | 2228.929 km | 2334.931 km | 2317.722 km | 2317.722 km |
| Distance 1 m | 0.001000 km | 0.001000 km | 0.001001 km | 0.001000 km |
| Distance 1 cm | 0.000010 km | 0.000010 km | 0.000000 km | 0.000010 km |
The calculations were performed with a program written in C++ (Sourcecode at GitHub).
For distances in the range of a few meters to kilometers, the four variants are practically equivalent in terms of their accuracy. With distances on a European scale, however, there are large differences, so that the exact methods should always be used here, taking into account the surface of the sphere. For very small distances in the range below one meter, the calculation according to the spherical law of cosines exhibits numerical instability, which leads to incorrect results. The Haversine formula delivers a correct result for both large and very small distances and thus represents the optimum.
Supplement 1: Calculation of distance for ellipsoids
The previous considerations have always assumed that the earth is a sphere. However, this is not the case. Rather it is an irregularly shaped Geoid. It can be approximated with the figure of an Ellipsoid. An ellipsoid is determined by the length of its semi-major axis (the equatorial radius) and semi-minor axis (the polar distances).
Unfortunately, there is no simple formula for the ellipsoid analogous to the cosine rule for the sphere. The calculation of distances on the surface of an ellipsoid is much more complicated. Additional there is not only "the one ellipsoid of the earth" but dozens of them. It depends on the location on earth which ellipsoid approximates best the actual surface of the earth. The parameters of this ellipsoid (length of axis and displacement of the center) are often understood by the term "geodetic system" or "geodetic datum". Several hundred different exist. A de facto standardization has been achieved by the spread of global Global Positioning Systems (GPS), which uses the WGS84 reference ellipsoid.
The development of a tool for accurate distance determination for all kinds of ellipsoids and geodetic datums is therefore complex matter. Luckily, such tools already exist. In this article is PROJ.4 - Cartographic Projections Library the tool of choice. Proj.4 is completely available as source code and binary distributions for Linux and Windows. There is also the Java Map Projection Library which is a partial port of Proj.4 to Java.
The command-line tool geod included in the package is used for distance calculation. The call
geod +ellps=WGS84 +units=km -I
is expecting the input of the coordinates of the two points in the format lat1 lon1 lat2 lon2 as decimal degrees, for example:
49.9917 8.41321 50.0049 8.42182
The last value of the output is then the distance in kilometers. The calculatation uses the WGS84 ellipsoid, i.e. the input coordinates have to be determined in the WGS84 system. For the original GPS coordinates that is always the case.
In reviewing the examples from above the result for the short distance in Rüsselsheim is again 1.593 km. The distance Berlin - Lisbon is now calculated with 2318.217 km. The exact method with the sphere triangle is therefore next to approximately 500 meters. This means in relation to the distance just an error of 0.02%.
Supplement 2: Using other map grid
The simplified methods of plane trigonometry are sufficient to determine short distances. However, a shortcoming of the formulas given is the need to have to be multiplied by the "odd" values for the distances between the parallels and meridians. In addition, the distances between the meridians are not constant. It would be much easier if you could use coordinates that do not have these disadvantages and can be directly converted into distances.
Such coordinate systems already exist. The most common are the Gauss-Krüger coordinate system in Europe and the Universal Transverse Mercator coordinate system (UTM) world-wide. Both coordinate systems allow to map small regions of the earth's surface into a plane, so that they can be overlaid with a rectangular coordinate system.
These coordinates are then no longer measured in degrees, but in meters. Instead of latitude and longitude they usually bear the name Northing and Easting.
The tool GeoPosition enables the conversion of geographical coordinates into UTM. For the two known places in Rüsselsheim it delivers:
| Place | Easting | Northing UTM Zone 32U |
|---|---|---|
| Rüsselsheim Station | 457939 m | 5537873 m |
| Rüsselsheim Opel bridge | 458568 m | 5539336 m |
Since the coordinates are in meters and are in the same UTM zone, one can calculate the distance immediately with the Pythagorean theorem and the result is again the known value of 1.593 km.
In fact, these coordinates are so convenient to use that most topographic maps, if they only show a relatively small area, contain an UTM grid instead of "odd" geographical coordinates